Anschauliche Mathematik

Elastisches Seil mit Last und Dämpfung

Wie bewegt sich ein elastisches Seil unter gleichmäßiger Streckenlast, falls es an beiden Enden bei $x=0$ und $x=L$ fest auf gleicher Höhe eingespannt ist? Dieses Problem führt auf eine partielle Differentialgleichung (PDG) der Form $$ \frac{\partial^2 u}{\partial t^2} = c^2\cdot\frac{\partial^2 u}{\partial x^2} - b\quad\mbox{bzw.}\quad u_{tt} = c^2 u_{xx}-b $$ wobei $c$ und $b$ zwei materialabhängige Größen sind. Eine solche PDG lässt sich mit verschiedenen Methoden analytisch lösen. Gemäß dem Ansatz von d'Alembert ergibt sich die Auslenkung $u(x,t)$ des schwingenden Seil, indem man zur stationären (= zeitunabhängigen) Ruhelage $w(x)$ eine nach links laufende Welle $f(x+c\,t)$ und eine nach rechts laufende Welle $f(x-c\,t)$ addiert: $$u(x,t) = w(x) + f(x+c\,t) + f(x-c\,t)$$

Nach dem Separationsansatz von Bernoulli erhält man das schwingende Seil auch auf einem anderen Weg, indem man zur stationären Ruhelage noch eine oder mehrere sog. "stehende Wellen" addiert: $$u(x,t) = w(x) + v_1(x,t) + v_2(x,t) + \ldots$$

Falls das elastische Seil zusätzlich noch gedämpft ist, dann wird die Auslenkung $u(x,t)$ durch eine PDG der Form $$ \frac{\partial^2 u}{\partial t^2} + 2\,\delta\,\frac{\partial u}{\partial t} = c^2\,\frac{\partial^2 u}{\partial x^2} - b $$ beschrieben, die mit analytischen Mitteln nur noch schwer zu lösen ist. In einem solchen Fall verwendet man ein numerisches Verfahren wie z.B. die Finite-Differenzen-Methode (FDM):

(bitte anklicken)

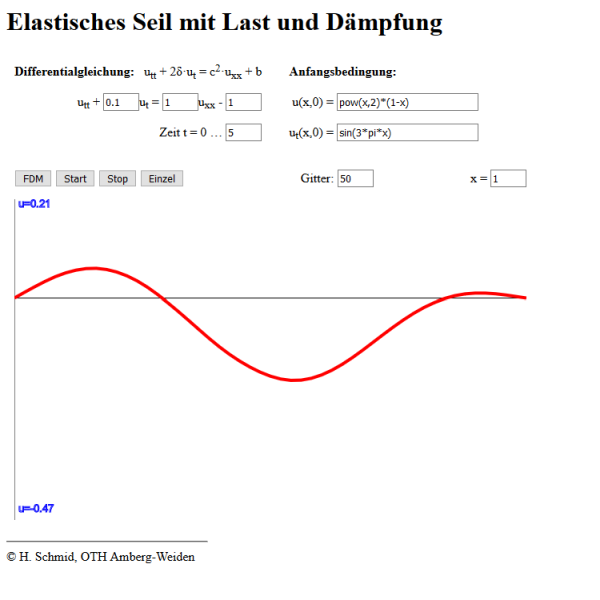
Anleitung: Die Koeffizienten $2\,\delta$ vor $u_t$ und $c^2$ vor $u_{xx}$ sowie die Konstante $b$ können direkt bei den entsprechenden Feldern in der PDG eingetragen werden. Die Grundlänge $L$ des Seils lässt sich bei $x=...$ angeben. Der simulierte Zeitraum $T$ wird bei $t=0...$ festgelegt, während im Eingabefeld "Gitter" die Anzahl $n$ der Gitterpunkte in $x$-Richtung für die FDM vorgegeben werden. Voreingestellt sind $L=1$, $T=5$ und $n=50$ Gitterpunkte. Darüber hinaus lässt sich die Ausgangsform des Seils zum Zeitpunkt $t=0$ im Feld $u(x,0)$ und die Anfangsgeschwindigkeit bei $u_t(x,0)$ eingeben. Hier sollten nur Funktionen verwendet werden, die allein von $x$ abhängen und an den Randpunkten $x=0$ sowie $x=L$ jeweils Nullstellen haben (andernfalls erhält man physikalisch unsinnige Ergebnisse). Die Funktionen werden in der bei Online-Plottern üblichen Form angegeben, z.B. cos(3*x) für $\cos 3x$ oder pow(x,2) für $x^2$, wobei pi für die Konstante $\pi$ verwendet werden kann. Der Button "FDM" übernimmt die ggf. neu eingestellten Werte und berechnet die Seilauslenkung mit Hilfe der Finite-Differenzen-Methode. Nach "Start" wird die Seilschwingung simuliert, und mit "Stop" kann die Animation angehalten werden. Der Button "Einzelschritt" führt jeweils nur einen einzelnen Zeitsprung aus, sodass man die Veränderungen des Seils verfolgen kann.

Beschreibung: siehe Buch "Mathematik für Ingenieurwissenschaften: Vertiefung", Kapitel 6, Abschnitt 6.3