Anschauliche Mathematik für IngenieureSimulationen & Visualisierungen
Die Eulersche Formel ist ein wichtige und (vor allem auch in der Elektrotechnik) häufig verwendete Beziehung zwischen komplexen Zahlen. Sie besagt \(e^{i\varphi} = \cos\varphi + i\sin\varphi\). Wie kommt diese Gesetzmäßigkeit zustande? Auf der linken Seite steht die (natürliche) Exponentialfunktion, welche für reelle Exponenten \(x\in\mathbb{R}\) definiert ist durch $$ e^x := \lim_{n\to\infty}\left(1+\frac{x}{n}\right)^n $$ Ersetzt man hier \(x\) durch \(i\,\varphi\), dann kann man die Exponentialfunktion auch für imaginäre Exponenten festlegen: $$ e^{i\varphi} := \lim_{n\to\infty}\left(1+\frac{i\varphi}{n}\right)^n $$ Das geogebra-Applet zeigt, dass die Potenz im Ausdruck auf der rechten Seite für steigende Werte \(n\) immer mehr in die komplexe Zahl \(\cos\varphi + i\sin\varphi\) übergeht: $$ \left(1+\frac{i\varphi}{n}\right)^n \to \cos\varphi + i\sin\varphi\quad\mbox{für}\quad n\to\infty $$
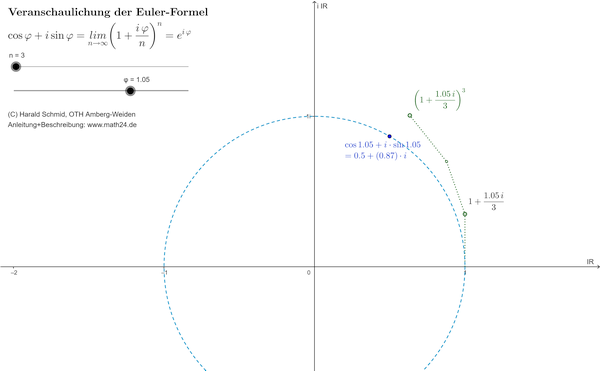
Anleitung: Das Argument \(\varphi\) sowie der Exponent \(n\) können über die Schieber eingestellt werden. Der blaue Punkt ist die komplexe Zahl \(\cos\varphi + i\sin\varphi\), während die grünen Punkte den Potenzen \((1+i\varphi/n)^k\) für \(k=1,\ldots,n\) entsprechen. Der letzte Punkt \((1+i\varphi/n)^n\) in dieser Reihe nähert sich mit steigendem Wert \(n\) immer mehr dem blauen Punkt an.
Beschreibung: siehe Buch "Mathematik für Ingenieurwissenschaften: Grundlagen", Kapitel 5, Abschnitt 5.2.3