 Anschauliche Mathematik für Ingenieure
Anschauliche Mathematik für IngenieureSimulationen & Visualisierungen
Dieses geogebra-Skript zeigt anhand einer Rechtecksschwingung und einer Dreiecksfunktion den Übergang von der Fourier-Reihe zur Fourier-Transformation. Die \(2L\)-periodische Rechtecksfunktion mit der Höhe \(h\) und der Breite \(2\,a\) lässt sich durch die Partialsummen der Fourier-Reihe $$ f(x) = \frac{a\,h}{L} + \sum_{n=1}^N\frac{2\,h\sin\frac{an\pi}{L}}{n\,\pi}\cdot\cos\frac{n\,\pi\,x}{L} $$ annähern, welche für \(N\to\infty\) immer mehr in die rechteckige Form übergeht (an den Sprungstellen ist das Gibbssche Phänomen des Überschwingens gut zu erkennen). Die \(2L\)-periodische Dreiecksfunktion wiederum kann man durch die Fourier-Reihe $$ f(x) = \frac{1}{L} + \sum_{n=1}^N\frac{2L\left(\cos\frac{n\pi}{L}-1\right)}{n^2\pi^2}\cdot\cos\frac{n\,\pi\,x}{L} $$ für \(N\to\infty\) approximieren. Das Spektrum der Funktion \(f(x)\) ist im unteren Bild zu sehen. Für \(L\to\infty\) geht die periodische Rechtecksschwingung in einen einzelnen Rechtecksimpuls bzw. die periodische Dreiecksfunktion in einen einzelnen Dreiecksimpuls über, und aus dem diskreten Spektrum wird ein kontinuierliches Spektrum.
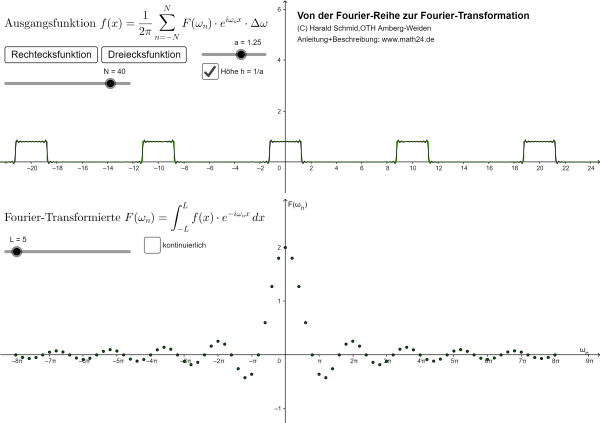
Anleitung: Im oberen Fenster kann man die halbe Breite \(a\) und wahlweise die Höhen \(h=1\) oder \(h=1/a\) für die Rechtecksfunktion einstellen. Die Dreiecksfunktion dagegen hat die feste Basis und Höhe \(2\). Mit dem Schieber für \(N\) lässt sich die Anzahl der Summanden in der Fourier-Reihe einstellen. Die halbe Periodenlänge \(L\) wird durch den Schieber im unteren Fenster festgelegt. Beobachtung: Das diskrete Spektrum wird mit steigendem Wert \(L\) immer "dichter". Der Grenzübergang \(L\to\infty\) führt dann zum kontinuierlichen Spektrum, welches durch ein Kontrollkästchen eingeblendet werden kann.
Beschreibung: siehe Buch "Mathematik für Ingenieurwissenschaften: Vertiefung", Kapitel 4, Abschnitt 4.5.3 - 4.5.4