 Anschauliche Mathematik für Ingenieure
Anschauliche Mathematik für IngenieureSimulationen & Visualisierungen
Der Krümmungskreis einer Funktion \(y=f(x)\) für \(x\in D\subset\mathbb{R}\) an einer Stelle \(x_0\in D\) ist derjenige Kreis, welcher den Funktionsgraphen in einer Umgebung von \(x_0\) bestmöglich annähert. Wie aber findet man diesen Krümmungskreis von \(y=f(x)\) bei \(x_0\)? Allgemein ist der Mittelpunkt eines Kreises immer auch der Schnittpunkt zweier beliebiger Normalen (= Geraden senkrecht zu den Tangenten) an zwei unterschiedlichen Stellen auf dem Kreisrand. Beim gesuchten Krümmungskreis sollen der Kreisrand und der Funktionsgraph von \(y=f(x)\) in einer Umgebung von \(x_0\) möglichst gut übereinstimmen. Der Mittelpunkt des Krümmungskreises ist dann näherungsweise der Schnittpunkt der Normalen zu \(y=f(x)\) bei \(x_0\) und bei einer benachbarten Stelle \(x_0+\Delta x\). Für \(\Delta x\to 0\) geht dieser Normalenschnittpunkt \(N\) über in den Mittelpunkt \((x_K,y_K)\) des Krümmungskreises mit dem Radius \(\rho\). Falls \(y=f(x)\) zweimal differenzierbar ist und \(f''(x_0)\neq 0\) gilt, dann erhält man hierfür die Formeln $$ x_K = x_0 - \frac{f'(x_0)\left(f'(x_0)^2+1\right)}{f''(x_0)},\quad y_K = f(x_0) + \frac{f'(x_0)^2+1}{f''(x_0)},\quad \rho = \frac{\sqrt{\left(f'(x_0)^2+1\right)^3}}{\left|f''(x_0)\right|} $$
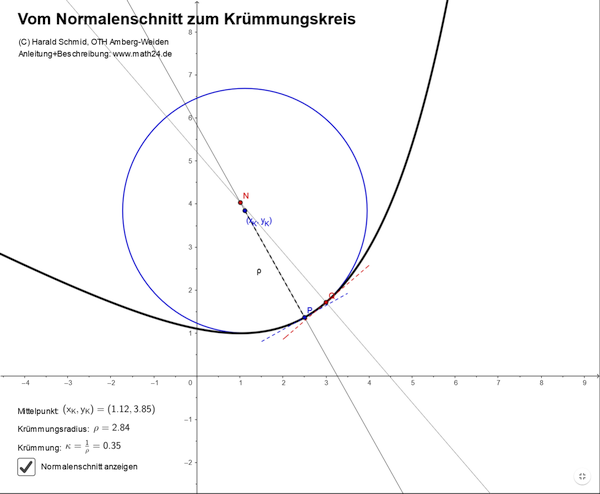
Anleitung: Falls "Normalenschnitt anzeigen" gewählt ist, kann man neben dem Punkt \(P=(x_0,y_0)\) noch einen benachbarten Punkt \(Q\) längs dem Graphen von \(y=f(x)\) verschieben. Sobald sich \(Q\) dem Punkt \(P\) nähert, dann geht der Normalenschnittpunkt in den Mittelpunkt \((x_K,y_K)\) des Krümmungskreises über.
Beschreibung: siehe Buch "Mathematik für Ingenieurwissenschaften: Grundlagen", Kapitel 6, Abschnitt 6.4.2