 Anschauliche Mathematik für Ingenieure
Anschauliche Mathematik für IngenieureSimulationen & Visualisierungen
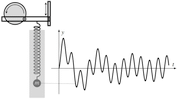
beschreibt die Bahnkurve eines Fadens, welcher straff gespannt von einer Rolle mit dem Radius \(R\) abgewickelt wird. Sie lässt sich in Parameterform mit den Koordinatenfunktionen $$ x(t) = R\cdot(\cos t + t\sin t),\quad y(t) = R\cdot(\sin t − t\cos t),\quad t\in[0,\infty) $$ darstellen. Bei der Evolventenverzahnung, einer der wichtigsten Verzahnungsarten im Maschinenbau, sind die Flanken des Zahnrads gemäß einer Kreisevolvente ausgebildet:

Weitere Details zu dieser Evolventenverzahnung findet man u.a. im gleichnamigen Wikipedia-Artikel.
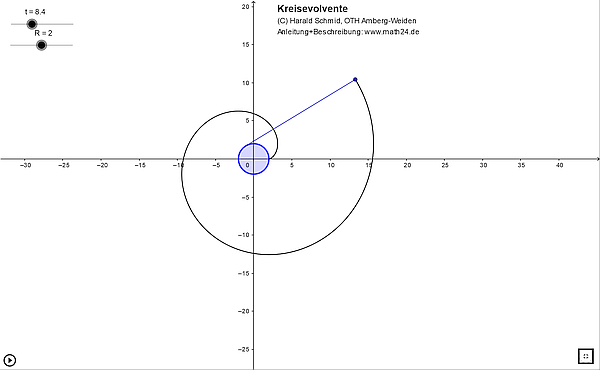
Anleitung: Mit ▶ wird der Faden ab- und wieder aufgewickelt, wobei der Radius der Rolle verändert werden kann.
Beschreibung: siehe Buch "Mathematik für Ingenieurwissenschaften: Grundlagen", Kapitel 6, Abschnitt 6.5.1